Det här fick man lära sig i "Elkrets C".
I korthet så visar cirkelbågarna i Smith-diagrammet som går igenom centrum
konstant resistans i ett Smith-diagram för impedans (=serieekvivalenter) och cirkelbågarna
som inte går genom centrum konstant reaktans, med induktiv i den övre halvan och kapacitiv i den nedre
När man sätter in en serieinduktans så kommer man att röra sig medurs utefter en
konstant-resistans cirkel, medan en seriekapacitans medför moturs rörelse.
Man måste hålla i minnet att det som används i Smith-diagrammet är "normaliserade", alltså multiplar av den resistans som man valt att utgöra origo i diagrammet.
Denna är vanligen 50 ohm.
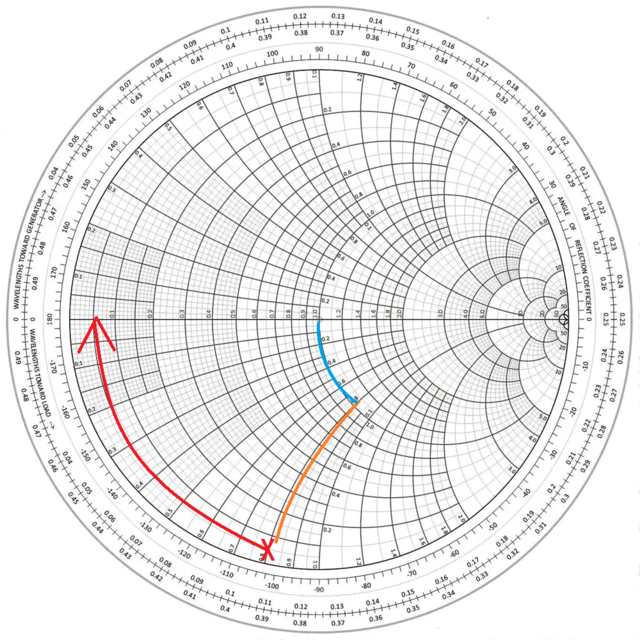
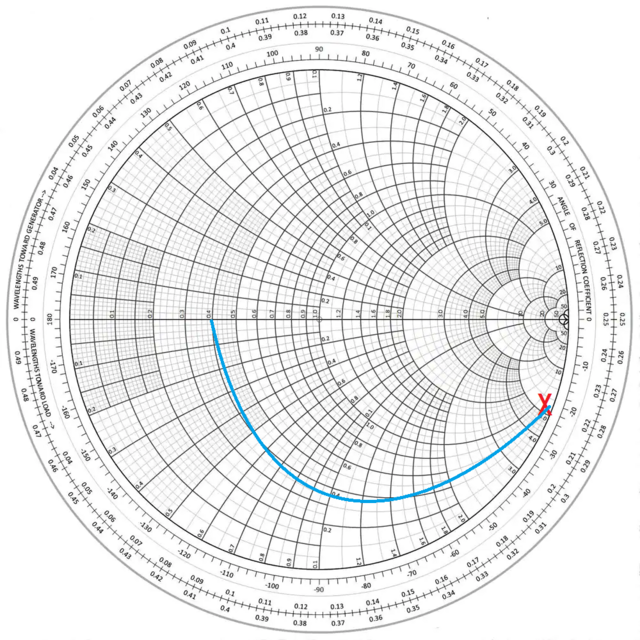
Om vi tittar på ditt exempel så startar vi med en antennimpedans som jag lite godtyckligt satt till 35 ohm realdel och -720 ohm imaginärdel. Detta blir normaliserat 0,7-j14,4.
Man får leta reda på den cirkelbåge som motsvarar 35 ohm och följa den tills man hittar
den punkt där den skär bågen som motsvarar -j720 ohm. Detta är DP1 i plotten.
Sedan har jag representerar förlusterna i spolen med en serieresistans av 2 ohm vilket blir DP2.
Därefter läggs serieinduktansen till, och då färdas man efter bågen 35+2 =37 ohm.
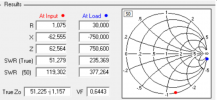
När sedan 720 ohm positiv reaktans har lagts till så blir impedansen i DP3 rent reell och 37 ohm.
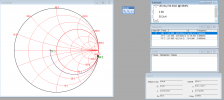
Om man önskar anpassa antennens impedans i exemplet till exakt 50 ohm så behövs en komponent till; en parallellkapacitans.
När man även använder parallellkomponenter så behövs den andra varianten av Smith-diagram, den som hanterar admittanser.
Detta är spegelbilden av impedansdiagrammet, och cirkelbågarna motsvarar konstant konduktans resp. susceptans. Dessutom blir rörelserna i diagrammet också spegelvända, så
en parallellkapacitans medför medurs rörelse och en parallellinduktans moturs.
För att göra detta anpassningsnät så måste vi först använda så mycket serieinduktans
att vi kan nå den admittanscirkel som motsvarar 1/50 ohm eller 20 mS och sedan färdas medurs efter den. Detta blir den nya DP3.
Sedan läggs så mycket parallellkapacitans till så att vi når origo i diagrammet eller DP4.

 qucsstudio.de
qucsstudio.de