Rothammel förkortad dipol för 80 och 40 m - funktion?

S

SA0BJL

Well-Known Member
Jag har byggt den här antennen som beskrivs i "Antennenbuch". Ett ben består av 10,97m ledare, en spole på 120uH och 1,53m ledare. Jag använde aningen andra mått, men har konstaterat att den täcker 40 meter och en del av 80 meter.

Men jag är inte riktigt på det klara med hur det fungerar. En förkortad 80m dipol med förlängningsspole förstår jag, men hur fungerar den som 40m dipol? Fungerar spolen som trap pga distribuerad kapacitans, eller finns det någon annan förklaring? Min tyska är inte så bra, men vad jag kan förstå av Rothammel har man kommit fram till måtten genom experiment. Någon som kan utbilda mig lite?

73 de Lars
 
Måtten skvallrar om att den är en "trapdipol", ehuru oavsiktlig.
Spolarna blir resonanta på 7 MHz genom sina distribuerade kapacitanser.

Förmodligen är den mycket känslig för omgivningens inverkan, p.g.a. att
förlängningsspolarna har en ganska stor mantelarea och därigenom en stor kapacitans mot omgivande objekt.

73/
Karl-Arne
SM0AOM
 
SM0AOM said:
Måtten skvallrar om att den är en "trapdipol", ehuru oavsiktlig.
Spolarna blir resonanta på 7 MHz genom sina distribuerade kapacitanser.

Förmodligen är den mycket känslig för omgivningens inverkan, p.g.a. att
förlängningsspolarna har en ganska stor mantelarea och därigenom en stor kapacitans mot omgivande objekt.

73/
Karl-Arne
SM0AOM
Click to expand...

Tack Karl-Arne! Det där med känslig är inte optimalt, jag byggde den för att ha som portabeldipol, så förhållandena kommer variera varje gång...

En äkta trap borde alltså vara bättre då man kontrollerar kapacitansen bättre.

Men om jag ändå vill räkna lite på den: hur beräknar jag distribuerad kapacitans i en spole med givna mått?
 
SM0AOM said:
Måtten skvallrar om att den är en "trapdipol", ehuru oavsiktlig.
Click to expand...

Wow! "ehuru" ett allt för sällan använt och vackert ord som, icke förty, har sin givna plats i det svenska mer förädlade språkbruket... ;-)

73/Lasse
 
Den bästa och mest begripliga diskussionen som jag sett om distribuerad kapacitans hos induktanser kan läsas här:

http://www.g3ynh.info/zdocs/magnetics/appendix/self_res/self-res.pdf

Det kommer ut några semi-empiriska samband mellan spolens dimensioner och den distribuerade kapacitansen.

Annars kan man använda G4FGQ:s DOS-program solnoid3.exe för
att få en uppskattning av kapacitansen och självresonansfrekvensen hos enkellagriga spolar.

73/

Karl-Arne
SM0AOM
 
Jag har provat en antenn med dubbla måtten och spolar på 450 µH, den gick på 80 m och 160 m. Spolarna såg jag som HF-drosslar och jag kollade aldrig deras resonanser.

Lennart
 
SM0AOM said:
Den bästa och mest begripliga diskussionen som jag sett om distribuerad kapacitans hos induktanser kan läsas här:

http://www.g3ynh.info/zdocs/magnetics/appendix/self_res/self-res.pdf
Click to expand...
Det var en riktigt bra artikel som bl.a. sköt ett stort hål i artikeln av
Grandi et al som jag länkade till ovan. Det var bra historiska återblickar på andra teorier också, och underhållande beskrivningar av forskningsfusk.

SM0AOM said:
Annars kan man använda G4FGQ:s DOS-program solnoid3.exe för
att få en uppskattning av kapacitansen och självresonansfrekvensen hos enkellagriga spolar.
SM0AOM
Click to expand...

Det jag fastnade för i artikeln är att medan det är enkelt att räkna ut kapacitansen från egenresonansen, så är det svårt att räkna ut egenresonansen från kapacitansen. Detta pga det stora förhållandet L/C så att små variationer i C ger stora utslag i frekvensen. Min ide var ju att kunna räkna ur resonansfrekvensen om jag kunde ta reda på kapacitansen, så den iden faller.

Men om nu egenresonansen kan räknas som halvvågsresonansen för längden på spolens ledare så har man den ju i alla fall utan omvägar. Frågan är bara vad jag gör med detta. Om jag förstått det rätt så är det inte kritiskt vad "trapen" har för resonansfrekvens, det skulle kunna fungera med någon frekvens mellan 40 och 80 metersbanden?
I så fall skulle man kunna designa spolen för den förkortade 80 metersdipolen och sedan kontrollera om resonansfrekvensen hamnade i ett fungerande område för 40 metersdipolen.

Nu är jag ute på tunn is, så det är bara att hoppa in och förklara var jag tänker fel!

73 de Lars
 
SM5DFF said:
Jag har provat en antenn med dubbla måtten och spolar på 450 µH, den gick på 80 m och 160 m. Spolarna såg jag som HF-drosslar och jag kollade aldrig deras resonanser.

Lennart
Click to expand...

Just så fungerar det.
Man vill att spolens egenresonansfrekvens ska ligga så högt som möjligt.
Det är ju den induktiva reaktansen man vill åt.
Enkelt förklarat så kan inte antennströmmen i SA0BJL´s antenn passera spolen på 40m och följaktligen så "syns" inte den yttre tråden.

Martin E. Meserve - K7MEM - Electrically Shortened Center-Fed Half-Wave Dipole ( 3-30 MHz )

/Micke
 
Last edited:
SA0BJL said:
Men om nu egenresonansen kan räknas som halvvågsresonansen för längden på spolens ledare så har man den ju i alla fall utan omvägar. Frågan är bara vad jag gör med detta. Om jag förstått det rätt så är det inte kritiskt vad "trapen" har för resonansfrekvens, det skulle kunna fungera med någon frekvens mellan 40 och 80 metersbanden?
I så fall skulle man kunna designa spolen för den förkortade 80 metersdipolen och sedan kontrollera om resonansfrekvensen hamnade i ett fungerande område för 40 metersdipolen.
Click to expand...

Det blir väldigt svårt att "designa" en sådan antenn. Många inbördes samverkande faktorer som är svåra att modellera kommer att påverka.
Det som går att säga är att den beskrivna antennen är en form av "urartad" förlängd dipolantenn med förlängningspolarna mycket nära antenntrådens ändar.

Teorin för förlängda dipoler säger att induktansen (eller den induktiva reaktansen) för en sådan spole växer exponentiellt när dess placering närmar sig trådänden. Tänker vi nu oss extremfallet att spolen är självresonant så är
dess induktans oändlig, och den kommer att avsluta tråden på samma sätt som en isolator.

Nu är det i praktiken omöjligt att göra ideala sådana spolar, och man får då nöja sig med ett belopp hos spolimpedansen på kanske 10000 ohm i bästa fall.

Detta kan jämföras med antenntrådens medelimpedans på omkring 800 ohm för normalgrova trådar. Begreppet "medelimpedans" kommer ur Schelkunoffs banbrytande arbete från 1941 som revolutionerade den dåtida antennteorin. Schelkunoff använde en mycket giltig analogi mellan antenner och andra transmissionsledningar.

När en våg som utbreder sig utefter antenntråden träffar på spolen kommer huvuddelen att reflekteras tillbaka på samma sätt som om det vore en isolator som satt där. Spänningsreflektionsfaktorn gamma kommer att vara grovt 0,85 så att ungefär 75 % av energin återreflekteras från spolen, vilket är fullt tillräckligt för att modellen ska vara giltig.

När arbetsfrekvensen är 3,5 MHz kommer spolen inte längre att vara i närheten av självresonans, utan den kommer att uppträda som den induktans den är, och introducera ett positivt fasskift hos antennströmmen, vilket innebär en
förlängning av antennen.

En uppskattning kan göras genom att plotta antennkonfigurationen i ett Smith-diagram normaliserat till antennens medelimpedans 800 ohm. Grovt får man resonans på 3,5 MHz med 11 m tråd, 120 µH förlängningsspole samt 2,4 m tråd seriekopplat vilket ligger nära verkliga värden.

P.g.a känsligheten för omgivningens inflytande blir det vanskligt att försöka konstruera en antenn att detta slag bara via beräkningar.

73/
Karl-Arne
SM0AOM
 

Attachments

  • smith_rothammel.jpg
    smith_rothammel.jpg
    94,7 KB · Views: 116
Last edited:
SM0GLD said:
Just så fungerar det.
Man vill att spolens egenresonansfrekvens ska ligga så högt som möjligt.
Det är ju den induktiva reaktansen man vill åt.
Click to expand...
OK, men det finns två olika designprinciper för traps. En är att lägga resonansfrekvensen mellan banden så att man får induktiv loading på ena bandet och kapacitiv på det andra. Jag skummade igenom ARRL Antenna Book lite snabbt, och de anger att en fördel är lägre strömmar i trapen och därmed lägre förluster. Men det krävs ändå lite tanke bakom komponentvalen, så man har inte så stor frihet som jag tänkte först.

SM0AOM said:
Det blir väldigt svårt att "designa" en sådan antenn. Många inbördes samverkande faktorer som är svåra att modellera kommer att påverka.
...
P.g.a känsligheten för omgivningens inflytande blir det vanskligt att försöka konstruera en antenn att detta slag bara via beräkningar.
Click to expand...
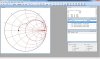
Jag köper att det inte går att designa den här antennen ingenjörsmässigt, men man borde väl kunna komma i närheten? Jag tycker din simulering med Smithdiagrammet och värdena så nära tyder på det. Jag har provat att räkna lite i alla fall men får inte ihop siffrorna, så ni kanske kan hjälpa till och se om jag missförstått något?

Om jag börjar med att se antennen bara som en förkortad 80 metersdipol och försöker bestämma värdet på spolen: CT1EOJ har skrivit en artikel "Designing a shortened antenna" (QST oktober 2003). Om jag förkortar en 2*20,5 m dipol till de angivna måtten enligt hans process, får jag L=196uH. Är det någon som har synpunkter på den metoden, eller beror skillnaden (L=120uH) på att spolen ligger så nära änden på dipolen? Jag har använt följande värden:
f=3,55MHz
Antennhöjd h = 10m
Diameter på antenntråden d = 2mm
Z0=138*log(4h/d) = 593,5ohm
Beta1 (vid 1,53m) = 6,72 grader => X1= -j Z0*cot(Beta1) = -j5039 ohm
Beta2 (vid 9,53m) = 41,8 grader => X2= -j663 ohm
X = 5039-663=4376 ohm => L=196uH

Rothammel anger L=120uH och N=200 varv, d=1mm och 25mm PVC-rör =>r=13mm (l blir 250mm). Jag räknar L=0,001*N^2*r^2 / (228r+254l) = 102uH. Är det fel i min beräkning?

Till sist räknade jag spolens egenresonans utifrån att längden på ledaren = en halvvåg. Lamda = 2*N*PI*D = 32,7m => f=9,18 MHz. Det är inte där jag förväntade mig...

Även om det inte går att räkna på just den här antennen så är jag intresserad av om jag missförstått någon formel eller teori.

/Lars
 
Rothammel skrev att man kommit fram till måtten genom experiment, och det tror jag på i mycket hög grad.

T.ex. ger traditionella beräkningar av induktans som Wheelers formel induktansvärdet vid så låga frekvenser där man kan försumma inverkan av distribuerade kapacitanser, så värdet 120 µH kan vara uppmätt på någon annan frekvens.

Sedan finns det lite olika synsätt på vilka värden medelimpedansen hos en antenntråd har, det värde som CT1EOJ använt kommer ur en inte alltför bra approximation av impedanser hos trådar över oändligt stora jordplan, medan
den approximation som jag använt kommer ur Schelkunoffs generalisering av den bikoniska antennen som inte påverkas av några jordplan.

Detta värde är nära dubbelt så högt som det som CT1EOJ använt.
(Hela resonemanget bakom detta finns att läsa i W6UYH:s artikelserie "Antenna - Transmission Line Analog" , Ham Radio Magazine 5/6 1977)

Olika värden på antenntrådens medelimpedans ger påverkan på längderna av trådarna. Dessutom tillkommer en kapacitiv last längst ut i ändarna av antennen som består av förlängningsspolarnas kapacitanser till omgivningen. Denna strävar att göra antennen kortare för en given resonansfrekvens.

73/

Karl-Arne
SM0AOM
 
Om jag minns rätt så är Walt Maxwell, W2DU, i sin bok Reflections II mycket kritisk mot att placera en stor förlängningsspole direkt under en kapacitanshatt på en antenn. - "That is strictly no-no" tror jag han säger, och skälet är att om spolen är dimensionerad så att den är nära självresonant på arbetsfrekvensen har dess impedans en ganska så stor resistiv komponent, men det flyter fortfarande ström genom den och förlusterna kan bli stora.

Det här går säkert bra att simulera med Eznec - enklaste försöksmodellen är en vertikal med kapacitanshatt (gör ett knippe korta radialer med radialfunktionen i Eznec och flytta dem till vertikalens topp) och en stor induktans direkt under kapacitanshatten. Modellera spolen som en LC-parallellkrets (välj ett Q-värde på ca 300 för spolen). Välj Mininec-jord för enkelhets skull och studera hur förlusterna i spolen varierar med frekvensen. Klargörande!

Walt Maxwell var vad somliga på den här listan skulle kalla "gammalt fossil" - han var 93 år när han avled 3 juli i år och man kan läsa en intressant runa på W2DU - Walt Maxwell

73 //Janne SM0AQW

PS - Det är inte alltid som Rothammel är något sanningsvittne! DS
 
Last edited:
Nu börjar poletten trilla ner! :) Jag ska se om det går att gräva fram de gamla HRM tidningarna med W6UYH' s artikel. När jag sökte på den hittade jag en annan tråd i det här forumet om att förkorta en vertikal. Där nämner du boken "Handbok of antenna design" och den verkar gå att köpa.

Tnx fer vy gd info!

/Lars
 
JanneG said:
Om jag minns rätt så är Walt Maxwell, W2DU, i sin bok Reflections II mycket kritisk mot att placera en stor förlängningsspole direkt under en kapacitanshatt på en antenn. - "That is strictly no-no" tror jag han säger, och skälet är att om spolen är dimensionerad så att den är nära självresonant på arbetsfrekvensen har dess impedans en ganska så stor resistiv komponent, men det flyter fortfarande ström genom den och förlusterna kan bli stora.
Click to expand...

Detta är en annan aspekt på saken. På både 3,5 och 7 MHz torde verkningsgraden med så stora induktanser ute i ändarna påverkas ganska mycket negativt.
Det som man vinner i strömarea med en rektangulär strömfördelning på antenntråden förloras genom förluster i förlängningsspolen.

"There is no such thing as a free lunch".

W2DU var en "riktig radioamatör", och ser man på bilderna av "shacket" så satt GR1606 impedansbryggan på en framträdande plats.

Det är lätt att inse varför.

RIP, Walt

73/
Karl-Arne
SM0AOM
 
Ja, W2DU han var en riktig kämpe, och dessutom spelade han trumpet i Alvino Rey´s storband 1946, Det bandet var bra på att spela Hawaii-låtar i swingstil (tror -3BDZ håller med?). Senare övergick Walt att spela bas(fiol) i mindre band.

meddelar Janne/SM0AQW
 
SA0BJL -- Lars,
mejla mig din e-mail adress så ska jag skic ka dig en bra skrift

73 Janne SM0AQW email sm0aqwATtelia.com
 
You must log in or register to reply here.
Back
Top