Komponentfattig "rörsändare"

[SM7EQL]

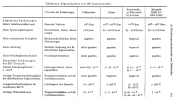
Slutsatser dragna: Magnetiska material bör om möjligt undvikas till förmån för luftlindade kopplingsnät.

Vad fick du för mätresultat på dina ferrittransformatorer med minimum loss pad metoden?

 

[SM7MCD]

För tio år sedan hade vi en "rörkurs" inom KRAS, och en pryl vi byggde var en sändare av typ från den finska "Kynnel". Med ett 6J6 fick man ibland 1 W uteffekt, men med ett QQE 04/15 kunde man plocka ut 10 W, samma med två 6AQ5. Allt byggt med bara tio delar + nätdel!

Men det roliga är att antennen ingår i svängningskretsen, och om det började blåsa bland antenntrådarna började tonen glida fram o tebaks i takt med vinden, vilket gav en intressant karaktär på tonen... typ ett långsamt svävande. Lite som vibrato på en Theremin.

Leif

 

[SA7ELF]

Vad fick du för mätresultat på dina ferrittransformatorer med minimum loss pad metoden?

Jag har inte haft möjlighet att testa än. Min verkstad där jag har all utrustning är knappt 4 mil söder om mitt QTH så det är främst på helgerna jag har möjlighet att fortsätta med mina experiment och de två kommande helgerna är uppbokade på annat håll så det kan dröja lite innan jag kan återkomma med mätresultat

 

[SM0AOM]

Men det roliga är att antennen ingår i svängningskretsen, och om det började blåsa bland antenntrådarna började tonen glida fram o tebaks i takt med vinden, vilket gav en intressant karaktär på tonen... typ ett långsamt svävande. Lite som vibrato på en Theremin.

Det här är mycket betecknande för "frisvängande" eller "ostabiliserade" sändare.
Förkrigsamatörerna, vilka gärna använde effektoscillatorer direktkopplade till antennerna







och även professionella råkade ut för detta fenomen.

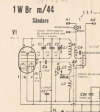
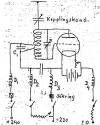
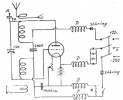
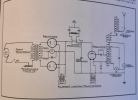Av den anledningen blev användningen av enrörssändare,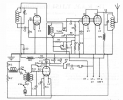
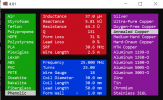
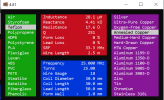
i synnerhet konverterade gnistsändare ganska kortvarig inom fartygsradion,
och man övergick snabbt till två-stegssändare MO-PA.



"Det var bättre förr..."

 

[SM7MCD]

Jag var och rotade lite bland delarna från KRAS-utbildningen där vi gick igenom hur man kan linda spolar och använda dessa i sändare. Den smala till vänster är "dålig", den i mitten är "bra", och den till höger är "bäst".

Dessa spolar användes på två 807r i PP, samt ibland med ett QQE06/40 med ca 100W ut på 2 - 20 MHz, och det är stor skillnad mellan dessa spolar.

 

[SA7ELF]

Jag var och rotade lite bland delarna från KRAS-utbildningen där vi gick igenom hur man kan linda spolar och använda dessa i sändare. Den smala till vänster är "dålig", den i mitten är "bra", och den till höger är "bäst".

Dessa spolar användes på två 807r i PP, samt ibland med ett QQE06/40 med ca 100W ut på 2 - 20 MHz, och det är stor skillnad mellan dessa spolar.

Mycket informativ bild. Tackar så hjärtligt. Gör det någon skillnad ifall sekundärspolen är utdragen över hela längden av primären? Eller är det samma tumregel som för större spolar att avståndet mellan varje varv bör vara ca en tråddiameter?

 

[SM6GPV]

"QRG?
Är jag på, eller i närheten av, något amatörband och i så fall, vilket?"

Jag hade några oavsiktliga "cross-band-QSO" sent 70-tal när jag trodde det var 70 cm men motstationen senare skickade QSL på 2m. Så går det när man har en Microwave Modules transverter 144-432 och har sin TS700 kopplad till en koaxialomkopplare med transverter och 2m-antenn som utgångar...

 

[SM0AOM]

Solfläcksmaximat runt 1970 fick en del liknande konsekvenser.

En del förhoppningsfulla trodde sig ha hört riktiga DX på 144 MHz, men vid närmare
undersökning visade de sig vara på transverterns MF på 28 MHz.

 

[SM7MCD]

Gör det någon skillnad ifall sekundärspolen är utdragen över hela längden av primären? Eller är det samma tumregel som för större spolar att avståndet mellan varje varv bör vara ca en tråddiameter?

Den bör ha samma delning som primären, dvs en tråddiameter tomrum mellan varven. Tips är att linda med två trådar och ta bort en när lindningen är säkrad. Lindar du med så tjock tråd som 2mm eller mer är det lättare att tätlinda och sedan "gänga" med en skruvmejsel (med rund klinga) längs med koppartråden tills mellanrummet blir lagom. Det brukar gå ganska snabbt att hitta lämplig diameter på klingan för att få en självbärande spole med rätt avstånd mellan varven.

 

[SM0GLD]

Tips är att linda med två trådar

Jag har lindat med dubbel tråd. Grästrimmerlina eller tjock fiskelina fungerar bra som distanstråd.
Man får leta lite så hittar man rätt dimensioner.

 

[SA7ELF]

Jag gjorde en snabb skiss på mätuppkopplingen;

View attachment 11086

De två motstånden utgör en s k minimum loss pad som för 50 ohm - 5000 ohm ger en minsta möjliga dämpning av 26,04 dB med ett SVF på 1,004:1 med ideala komponenter.

För lägre impedansomsättningar använder man i regel tre motstånd i Pi-koppling men för så här höga impedanser och dämpvärden så blir det tredje motståndet på många megaohm och kan utelämnas.

Det finns några saker att tänka på. För att dämpningen skall bli de beräknade 26 dB krävs att du använder små motstånd med kortaste möjliga anslutningstrådar. Du kan använda vanliga motstånd på låga frekvenser. Det är också viktigt att koppla ihop de fyra jordpunkterna i schemat till en gemensam punkt med så korta ledningar som möjligt eller använda ett RF-mässigt styvt jordplan.

För mätningar som dessa brukar man använda en testjigg som består av ett referensjordplan, t ex en al-plåt stor som ett A4-papper. Plåten fungerar som ett styvt lågimpedivt jordplan med försumbar induktans och ger stabila repeterbara mätresultat. Så här kan en sådan testjigg se ut. Det är samma grundprincip som de flesta tillverkarna av ferriter m m använder i sina utvecklingslab för att karaktärisera sina produkter. https://dx.sm7eql.se/?p=226

Dämpningen 26 dB är ganska hög och det betyder att strökapacitanser på den högohmiga sidan inkl de som finns i din transformator spelar in liksom det finns en liten kapacitans i motståndet som gör att resistansen för RF minskar en aning med ökad frekvens. Beroende på typ och storlek på motstånden kan de 26 dB t ex bli 24 dB på 30 MHz, 20 dB på 50 MHz osv. Därför kan du komma lite närmare sanningen om du kopplar ihop två likadana minimum loss pads rygg mot rygg och mäter den faktiska dämpningen som du sen delar med två och använder för att ställa om referensnivån i din VNA så att mätkurvan visar dämpningen i din transformator. Grundkalibreringen av VNA gör du i 50 ohm som vanligt.

Nu är 5000 ohm en väldigt hög impedans att hantera men du kommer att få en indikering på dämpningen i alla fall. Enklare mätinstrument i kombination med en olycklig mätuppkoppling kan ibland visa att en transformator visar lite förstärkning och då vet man att något är fel med mätuppkopplingen eller mätprincipen.

Ett annat alternativ är att koppla upp två identiska transformatorer via en dämpare med ca 10 dB dämpning eller mer. Dämparen stabiliserar impedansen och isolerar de båda transformatorerna så att oönskad återverkan blir försumbar.

View attachment 11087

Standardvärdena 10 k resp 6,8 k ger 9,63 dB dämpning och SVF 1,007:1 samt IN/UT impedans 5033,113 ohm med ideala komponenter.

De små kapacitanserna i motstånden som nämndes i förra mätuppkopplingen spelar in även här. För låga frekvenser under si så där 10 MHz och om du använder små motstånd med korta ben och ett styvt jordplan blir mätfelen små.

Men lägg en stund på detta och se vad du kommer fram till.

Jag har försökt googla minimum loss pad för att förstå mer om hur man kan beräkna och använda dessa men blir inte riktigt klok på värdena. Jag lyckas inte få till samma värden. Är den här kretsen ungefär korrekt:

 

[SM7EQL]

Jo det ser rätt ut. Du har beräknat en pad för 30 dB dämpning. Då blir de ideala resistansvärdena de som du visar. Kalkylatorn talar också om att den minsta möjliga dämpningen för en impedansomvandling mellan 50ohm och 5000 ohm är 25,999 dB.

Om du nu beräknar en ny pad med 26 dB dämpning så får du resistansvärdena shunt in 50,252 ohm serie resistor 4975,626 ohm och shunt ut >36 M, dvs shunten påverkar impedansen minimalt och kan därför utlelämnas.

Om vi håller oss till standardvärdena 50 ohm (som du får med 2 st 100 ohm i parallell) och 5 k (2 st 10 k i parallell) och skippar shunt ut så får man teoretiskt en pad som dämpar 26,04 dB och har 49,751 ohm ingångsimpedans och 5025 ohm utgångsimpedans. SVF blir med utgången terminerad i 5025 ohm 1,005:1 motsvarande RL 52,063 dB vilket är långt mycket bättre än din VNA klarar av att mäta.

 

[SM0AOM]

Det mest korrekta sättet är att betrakta en sådan "minimum loss pad" som en spänningdelare, där man får ut en viss fraktion av inspänningen.

Om man vill ha en sådan med minsta möjliga delningsfaktor och samtidigt har kravet på exakt 5000 ohm resistiv inimpedans blir denna ett seriemotstånd på 4950 ohm, om vi utgår från att inimpedansen hos VNA:n är exakt 50+j0 ohm.

Då blir delningsfaktorn 50/4950 = 0,0101 eller i amplitudmått -39,9 dB.
Nu protesterar läsaren, "39 dB är ju inte alls 26 dB!" men då har läsaren glömt bort
att "decibellen" är definierad som effektmått vid anpassning.

Den som läst sin Terman uppmärksamt, eller inte sov på föreläsningarna, har noterat denna passus på sidan 260:



En korrektionsfaktor mellan impedanserna, sista termen i nedanstående uttryck, behöver då introduceras;


vilket är 20 dB, så det blir -40+20 = 20 dB kvar.
Det saknas fortfarande 6 dB, och detta kommer sig av att effektmåttet
gäller vid anpassning, och då är polspänningen = EMK/2, eller - 6 dB.

Adderar vi ihop dessa termer blir det 26 dB totalt, och då går räkningarna "ihop".

Summan av allt detta är att den som håller på med dämpningsmätningar behöver
beakta alla faktorer; impedansnivåer, skillnaden mellan amplitud- och effektmått samt hur man anger spänningsnivåer, antingen som EMK eller polspänning vid anpassning. Vanligen är instrument kalibrerade i effektmått vid anpassning och då blir direkta jämförelser ofta missvisande.

 

[SM7EQL]

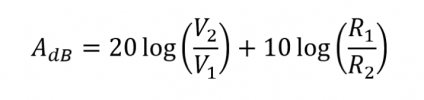
kravet på exakt 5000 ohm resistiv inimpedans

Det är exakt där vi har problemet. Transformatorns impedans för så stora impedansomsättningar som 100:1 är långt ifrån resistiv så mätvärdena får tas med en rejäl nypa salt. Det går dock alltid att optimera anpassningen i en given transformator genom att tillföra kapacitans på lämpliga ställen i kretsen. Ibland vinner man bara någon tiondels dB. I transistorsteg med bredbandstransformatorer för hela KV-området kan man ofta hämta hem någon eller några dB på de högsta frekvenserna genom att t ex lägga på lite kapacitans direkt över antennkontakten. I andra fall kan man lägga på en kapacitans över den andra lindningen för att antingen maximera uteffekten eller bara jämna till frekvensgången.

För en rörsändare där uteffekten är av primärt intresse torde dock en vanlig linkkopplad parallellkrets eller ett Pi-filter ge bäst resultat. Vi får naturligtvis förutsätta att spolarna lindas lagom glest på rätt sätt med tillräcklig tråddiameter t ex som MCD nämnde. Luftlindade eller lindade på stomme spelar mindre roll så länge som materialet i stommen inte är absorberar RF eller tillför andra problem. Keramik, Trolitul, Pertinax och vissa plaster är nog ganska säkra kort här.

I de applikationer jag använt liknande bredbandstransformatorer som ELF provar har jag först gjort en grov beräkning av impedansnivåerna och sedan systematiskt provat med olika varvtal och varvtalsförhållanden. Gör man det och noterar mätvärdena i en tabell eller ritar in mätvärdena efterhand i ett diagram på ett rutat kollegieblock så får man snabbt svar på vilka varvtal och omsättningar som ger mest utsignal, jämnast kurva eller vilket ferritmaterial som fungerar bäst eller rättare sagt ger den bästa kompromissen då alla parametrar inte låter sig optimeras samtidigt.

 

[SM5DFF]

Ta bort pertinax från listan på goda spolstommar, mätning med Q-meter har visat att det materialet förorsakar tydliga förluster.

 

[SA7ELF]

Hur är det med PP, PET och PVC? Min spolformare kommer troligen bli någon form av plaströr

 

[SM5DFF]

Jag har inte märkt någon försämring med plaströr som spolstomme.

 

[SM0AOM]

Som jag skrivit ett stort antal gånger tidigare så finns det mycket välgrundade orsaker
bakom varför man inte gör impedanstransformationer på 100:1 med fluxkopplade transformatorer vilka använder järnkärnor i HF-applikationer.

Vi som är "Ingeniure der alter Schule", alltså från tiden när man fick göra beräkningar med
sunt förnuft, nomogram, räknesticka, formelsamling och i någon mån "teknisk fickräknare" har fått lära oss detta i olika sammanhang, om inte annat genom egna surt förvärvade erfarenheter. Saker som går att göra i lågfrekvensområdet ganska enkelt, kan bli mycket svårrealiserbara, kanske t.o.m. omöjliga, i högfrekvenskretsar.

Ett annat av mina favorittuttryck är "engineering judgement", alltså att med utgående
från tumregler och egna samt andras erfarenheter göra underbyggda
bedömningar av kretslösningars realiserbarhet och egenskaper. Att tillägna sig sådant tar en viss tid, och ett av de bättre sätten är att faktiskt lyssna till sina mentorer...

"Pertinax" eller fenolvävplast finns i många former och färger, och mina egna erfarenheter är att förlustvinkeln kan sprida ganska mycket mellan sorterna. Dock så är det sällan som jag märkt något på frekvenser under 10 MHz c:a.

Rent allmänt så är plaster ganska lågförlustiga på kortvågsområdet.
Undantaget är den starkt polära plasten PVC, som börjar få dåliga HF-egenskaper redan vid några hundra kHz. Härdplaster som PP och PET har så små förluster i HF-området att de är svåra att mäta.

Som vanligt finns det vägledning i Taschenbuch






Man ser att glimmer, keramik med låga dieltal och opolära plastmaterial som
PTFE, polykarbonat och styrenplaster är överlägsna fibermaterial och pappersbaserade
pertinax-material. Däremot är glimmerbakelit ett bra isolationsmaterial för högfrekvens.

 

[SM0AOM]

Det finns något material om förluster i spolstommar,
och K6STIs program "coil" tar hänsyn till spolstommarnas
dielektriska förluster.

Programmmet är validerat med Q-metermätningar



Om man ersätter en fenolplast eller pappersbaserad pertinax-stomme
med teflon så förbättras Q från 131 till 251 på 25 MHz



Däremot har polypropylen och polystyren så låga förluster att de inte
påverkar Q, men PVC och plexiglas sänker Q med några %.

På lägre frekvenser är det en mycket mindre skillnad, och är knappast märkbart.

I ett anpassningsnät mellan 4000 och 50 ohm på frekvensen 3,5 MHz med ett arbets-Ql på 12 som har en induktans med 13 µH och ett komponent Qu av 207 ger en kretsverkningsgrad av (1-[Ql/Qu]) = 1-(12/207) = 0,94 eller -0,2 dB.

Detta kan försummas i det stora hela, och så låga förluster är mycket svåra
att åstadkomma med ferrittransformatorer.

 

[QRP]

1953 Novice Transmitter | OneTubeRadio.com

onetuberadio.com

//QRP