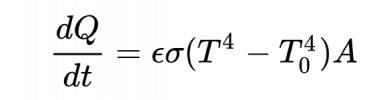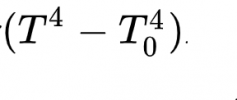Lyckligtvis talar vi eller PTS - ännu - inte om ERP. När detta blir ett faktum, som t.ex. ett resultat av allmänhetens "strålningsrädsla", kommer hela amatörradiokartan att ritas om. Det kommer sannolikt att bli effektgränser i häraden 50 W till en dipol på HF-banden, och kanske något 100-tal W ERP på VHF/UHF, ifall vi nu kommer att ha några sådana band kvar.
Dock förekommer det en missuppfattning i det citerade.
Det går inte alls att "grilla korv" även vid mycket stora antennvinster och därmed ERP-nivåer.
Orsaken är att det i exemplet totalt "bara" finns +40 dBm = 10 W effekt att tillgå. Korvgrillning med så låga effektnivåer tar obekvämt långa tider att realisera.
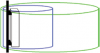
Vi kan för enkelhetens skull låta hela övningen försiggå på 3 cm eller 10 GHz, och antennvinsten på 40 dBd realiseras med en parabol med 0,7 m2 area eller en diameter på 1 m.
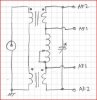
Vid vågledaränden som får utgöra matningshorn finns en effekttäthet på
10/(2*1) = 5 W/cm2 eller 50000 W/m2, vilket är långt över gränsvärdena, och man kan riskera att bränna sig om man har känslig hud.
Det är den största effekttäthet som går att åstadkomma någon stans i systemet.
Om vi tänker oss att parabolen belyses jämnt över hela ytan (orealiserbart i praktiken) har vi en effekttäthet på dess yta av 10/0,7 = 14 W/m2, vilket är över gränsvärdet men förmodligen inte direkt farligt.
Ställer man sig direkt framför parabolen kan det teoretiskt tänkas att det går att känna en uppvärmning, men korvar förblir råa.
Det +70 dBm eller 10 kW ERP som man teoretiskt tänker sig att kunna få kan bara existera på ett avstånd överstigande det där man kan börja försumma fasskillnaden mellan E och H, dvs där fjärrfältet är fullt utvecklat.
Detta avstånd ("Fraunhoferavståndet") är d > 2*D^2/(våglängden), där D är antennaperturens största utsträckning.
En härledning av detta samband finns i alla grundläggande läroböcker i mikrovågsteknik.
Med siffervärden insatta så blir avståndet d > 66 m.
En sfär med 66 m radie har en area = 56000 m2, och enligt definitionen av antennvinst kommer strålningen att koncentreras till en area som är 40 dB eller 10000 ggr mindre, dvs 5,6 m2.
Där kommer en effekttäthet S av c:a 10/5 = 2 W/m2 att finnas.
En typisk korv har en mantelarea av uppskattningsvis 0,2*0,02*3,14 = 0,012 m2 = A, varför den största effekt som den kan absorbera är P = S*A = 2*0,012 = 25 mW.
Termisk jämvikt torde uppstå i korven vid temperaturer som bara obetydligt överskrider omgivningens.
73/
Karl-Arne
SM0AOM
Ramlade över denna gamla tråd där effektmått diskuterades.
Sedan den skrevs för 12 år sedan har jag i min praktik fått en del ytterligare insikter i EMF-problematiken runt stora antenner vid höga frekvenser.
Det går att visa att fluxdensiteten framför en aperturantenn, t.ex. en parabol, inte kan överskrida 4 gånger effekttätheten vid ytan, oavsett avstånd.
Om vi använder detta värde, och låter allt annat vara oförändrat, såg går det dels att beräkna hur länge man behöver hålla en korv framför antennaperturen för att få den uppvärmd, och dels hur stor uppvärmningen blir.
Med de siffervärden som använts blir effekttillförseln ca 600 mW, alltså 0,6 J/s.
Nu har jag lyckats hitta, i en 70-tals uppsats om värmebehov vid tillagning, värmekapacitiviteten hos köttfärs, vilken är en huvudbeståndsdel i korv.
Den anges till 3300 J/K/kg i medeltal, och en typisk varmkorv väger c:a 90 g.
För att öka korvens temperatur med 1 K med en tillgänglig effekt av 0,6 J/s
behöver man vänta grovt räknat 500 sekunder. På 8 timmar så kommer man upp i en termperaturhöjning av 60 K över omgivningen, vilket väl får anses motsvara "genomstekt".
Men det finns ett litet problem med detta; korven förlorar även värmeenergi; genom ledning, strålning och konvektion.
När det gäller stillastående luft som omgivande medium så kan man som en första ordningens approximation försumma ledning och konvektion, men strålningsförluster kommer man inte ifrån. Hur stora dessa är bestäms av Stefan-Boltzmanns värmestrålningslag, och är proportionella mot den absoluta temperaturen upphöjt till 4.
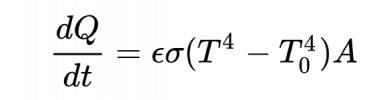
Med siffervärden insatta för tillgänglig effekt från parabolen dQ/dt 0,6 J/s och korvens mantelyta A, finner man att temperaturhöjningen
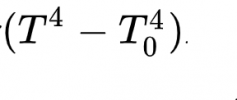
oavsett hur länge man väntar inte kan överstiga 9 K.
Korven förblir alltså rå.